Brace-aments are too much of a gamble
Wednesday, 7 September 2011
Brace-ament: n. Bracelet event which is essentially a crapshoot with an edge. The large field $1k and $1.5k WSOP events. Derived from the words “bracelet” and “donkament”.
Why have I defined a new term? Well, it’s fun. We poker players like new terms. Everyone wants to be the first person to say “triple range merge” legitimately in conversation.
After a summer of deep discussion at the Series on this subject, I thought it was about time I went into my lab and did some work on these “brace-aments”. Ordinarily, they wouldn’t be an issue. After all, there are all sorts of crapshoot tournaments around the World (take the EPT turbos, for example) and people are prepared to pay big bucks to play them. So expensive crapshoots aren’t new.
The trouble with brace-aments (and this is why they deserve their own special name) is that, because there’s a bracelet involved, people feel compelled to play them. You get all sorts of arguments regarding their good value which gloss over the fact that they are a complete gamble.
Let’s just remind ourselves of the single biggest reason tournaments are such a gamble in comparison with cash games. In cash games, for the most part, every time the button moves on, the luck counter is reset. Each hand is for a minimal, ever-fixed set of blinds and, should you wish to buy in as such, you start with the same stack.
In cash games, a cooler or a bad beat will have roughly the same negative effect on your bankroll if it takes place on hand number one or 1,000. Providing you stick to the same stakes, are careful about your game selection and make sure you are playing your A-game, in the long run, the luck factor will even out in cash games such that it’s not (for the good player) really gambling in the conventional sense.
In tournaments the stakes change. A cooler could happen for 10% of your stack or all of your stack. You could get a bad beat on a money bubble worth one third of a buy-in, or heads up in a big tournament for 100 buy-ins.
What does that mean in practice? Essentially it means that, in tournaments, the long run – the time needed for your skill factor to show through – is a lot longer. So long, in some cases, that it may be more than a lifetime. That’s called gambling.
As you can imagine, the worse the structure of a tournament, the bigger this effect becomes. Enter the brace-ament. Most people think that it is the structure of these tournaments that’s the biggest contributor to the luck factor. With 3,000 starting chips for a $1k event, the stack size isn’t great, but given there are one-hour blinds and the first level is 25/25, it’s not too bad. No, the real issue is field size.
There are various ways of testing how much field size affects the luck factor, but I want to use a tool I made last year for my article I’d Rather Be Lucky Than Good, Part 2, known as the “Vegas Trip Simulator”.
This simulator is a spreadsheet into which you plug the prize structure of a particular tournament, tell it your ROI and how many tournaments you want to play per “batch” (let’s say each batch is a trip to Vegas, so a batch-size of ten might be reasonable), and it will graph the distribution of your results. It does so by simulating 20,000 tournament results with your ROI, splitting them into batches of ten (or whatever). It will plot the results on a frequency graph like the one here:
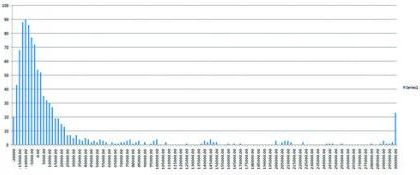
This is the frequency distribution graph for a 3,000 runner field, $1k buy in WSOP tournament and an ROI of 50%. The distribution is for 2,000 batches of ten – ie, 2,000 trips to Vegas playing ten such brace-aments each trip. I wanted to see this time just how big a gamble it was to keep entering these events (at $1k a pop, it all mounts up pretty quickly). You can see that the most likely result is that you will come back from your trip slightly down (even if you have an ROI of 50%).
The question regarding tournaments of this type specifically stems from an ongoing argument I had with Neil Channing about how much value there is in them. Granted, Neil has a point: as World Series events go, these are absolute cinches and the average standard is dreadful. He says that if you’re lucky enough to final-table one of these, you’ll be up against at least three players who don’t know what they’re doing.
All good so far, but I’m concerned that there are other factors here. First, there’s no question that the shallow starting stack means you’re gambling earlier. With deep stacks, you can afford to wait until the donkeys give their chips away without having to risk that much in the meantime (take the Main Event as an example). In brace-aments, you don’t have that luxury.
Second (and, as mentioned, more significantly), the size of the field means that you’re going to have to get very, very lucky to bink one of the big prizes. We’re back to that pesky issue of the long run again. Let’s put it simply. If you’re in a 100-runner tournament, the huge difference between first and second place (say 12 buy-ins) is down to a differential of 1% of the field. In a 1,000-runner tournament, the difference between first and second is maybe 80 buy-ins, and it’s based on a differential of 0.1% of the field. For the 3,000-runner brace-ament, the same difference is almost 200 buy-ins on a differential of 0.03% of the field. I don’t know about you, but that’s quite a gamble.
So, in plugging the numbers into the Vegas Trip Simulator this time, I’m not going to be as generous as last time with the ROIs. I think, as time goes on and databases recording people’s results get bigger, we’re no longer assuming huge ROIs such as 300% for the big players. In fact, I’m going to say that for brace-aments, the best players have an ROI of 100% and no more. Given what we’ve discussed about their crapshoot nature, I think that’s still pretty generous.
For the table below I’ve fed the prize pool and structure from event #34 of the 2011 WSOP into the simulator. This was a $1k event which had 3,144 runners and paid its bracelet winner, Mark Schmid, $488k for coming first (second place won 186 buy-ins fewer at $302k). I’ve then simulated 20,000 tournament results for players with an ROI of respectively 100%, 50%, 20%, 0% (i.e. break even after juice) and -20%. The table displays the percentage chances that each player would have made: (a) more than break even; (b) more than $100k; (c) more than $200k; (d) more than $300k, if he’d come back from the Series having entered ten brace-aments.
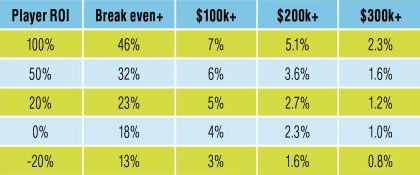
Interesting, huh? The thing that really struck me – and I have to say it’s almost comical – is that a player with a 50% ROI has only double the chances of making $100k+ (or indeed $300k+) as a player with a -20% ROI! To consistently post an ROI of 50% these days is no mean feat. If you’re such a player, it must be depressing to know that, in this type of event, you’re only twice as likely to come away with a big win as some schmuck who’s on a definite loser.
I’ve never simulated a player with a negative ROI before, and the results do actually figure. Even though our guy is a money-losing player, he’s still got a 3% chance of coming back from the Series over $100,000 up. Our hapless 100% ROI player – probably an A-lister like Mercier or Negreanu – has just over double (7%) his chances of posting the same result!
Note, also, the second left column: the chances of breaking even. As you might expect, this is the area where the better players show the greater discrepancy, but even then, the 50% ROI player has only a 32% chance of coming back from the Series having posted a positive overall result.
The message is quite simple: just because a field is weak, it doesn’t automatically follow that it’s a good gamble to enter the tournament, unless you have a few lifetimes and an infinite bankroll to spare. Field size is an important factor, as is tournament structure. Look for tournaments where you actually have a decent shot at exploiting the weakness of your opposition before having to go to the felt in a standard situation. And remember, the more times you have to go to the felt to get to the top of the pile, the longer the long run needs to be.